Related Publications:
(1) Parth Natekar, Manik Sharma. "Representation Based Complexity Measures for Predicting Generalization in Deep Learning." Winning Solution of the NeurIPS Competition on Predicting Generalization in Deep Learning (NeurIPS 2020), arXiv preprint arXiv:2012.02775 (Link)
(2) Yiding Jiang, Parth Natekar, et al."Methods and Analysis of The First Competition in Predicting Generalization of Deep Learning." Proceedings of the NeurIPS 2020 Competition and Demonstration Track, PMLR 133:170-190. (Link).
(1) Parth Natekar, Manik Sharma. "Representation Based Complexity Measures for Predicting Generalization in Deep Learning." Winning Solution of the NeurIPS Competition on Predicting Generalization in Deep Learning (NeurIPS 2020), arXiv preprint arXiv:2012.02775 (Link)
(2) Yiding Jiang, Parth Natekar, et al."Methods and Analysis of The First Competition in Predicting Generalization of Deep Learning." Proceedings of the NeurIPS 2020 Competition and Demonstration Track, PMLR 133:170-190. (Link).
We placed first at the NeurIPS 2020 competition for Predicting Generalization in Deep Learning (2020). My presentation at NeurIPS is available here. Our winning solution was based on two characteristics of the internal feature representations of deep networks - consistency and robustness. We achieved a high score of 22.92 on the final task. A gist of this and related ideas is below. A more detailed manuscript will be published as part of the NeurIPS 2020 post-proceedings, and the code is available on my github.
The generalization ability of deep neural networks, despite being significantly overparametrized, is a property of great interest from both theoretical and application perspectives. Understanding the factors behind generalization and creating practical measures which are predictive of generalization can lead to better network designs as well as a better theoretical understanding of this phenomenon.
Previous research has attempted to provide theoretical generalization bounds on the test error based on some intrinsic property of deep networks. However, many of the measures and bounds discussed above are not of practical use, and do not provide intuitive support to practitioners in terms of designing models which generalize better. We explore various complexity measures that are readily usable and that can predict the generalization performance of deep neural networks without the need for a test dataset.
The generalization ability of deep neural networks, despite being significantly overparametrized, is a property of great interest from both theoretical and application perspectives. Understanding the factors behind generalization and creating practical measures which are predictive of generalization can lead to better network designs as well as a better theoretical understanding of this phenomenon.
Previous research has attempted to provide theoretical generalization bounds on the test error based on some intrinsic property of deep networks. However, many of the measures and bounds discussed above are not of practical use, and do not provide intuitive support to practitioners in terms of designing models which generalize better. We explore various complexity measures that are readily usable and that can predict the generalization performance of deep neural networks without the need for a test dataset.
|
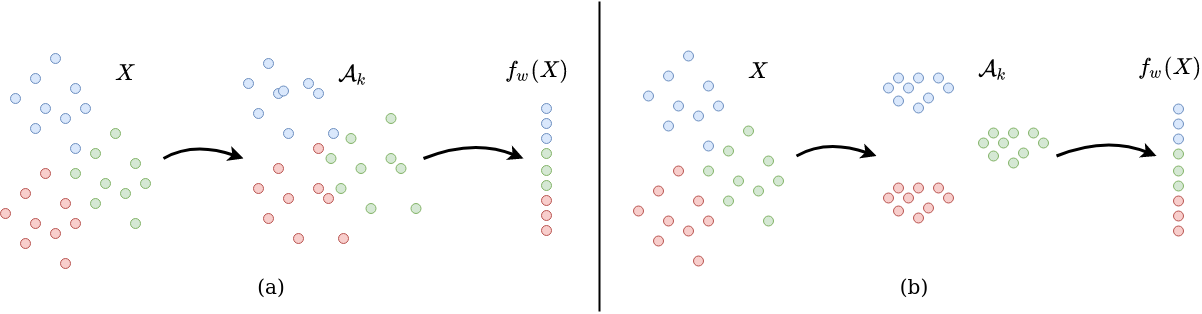
(1) Solution 1: Consistency of internal representations
Models which generalize well are likely to have more consistent feature representations. This follows from theories of how human beings generalize - through creating consistent symbolic representations of concepts. This is logical - if a deep neural network assigns the same label to two images, they have to converge into a similar representation at some stage of the network. Measuring the consistency of representation inside the network would then tell us about the generalization capacity of that network. We measure the consistency of internal representation using the Davies Bouldin Index to quantify the clustering quality of intermediate representations where the labels are the training labels. |
|
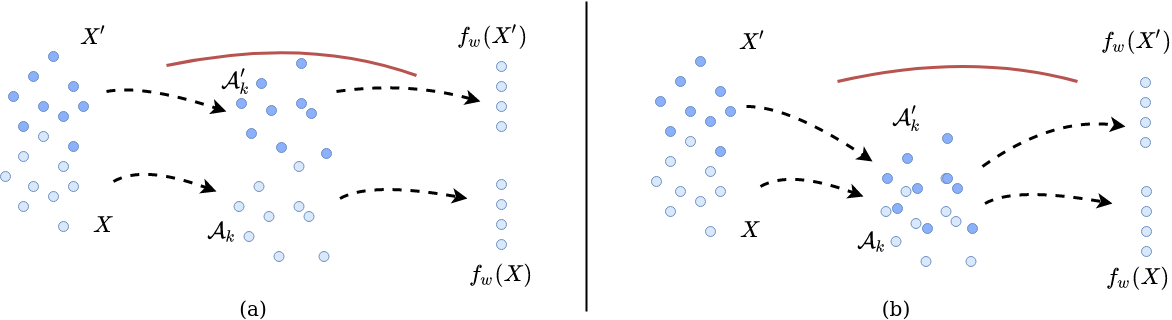
(2) Solution 2: Robustness to valid perturbations
Robustness of a model to plausible perturbations in the input space is another marker for generalization capacity. For measuring robustness of the network representations to valid or plausible perturbations, we use Mixup. In Mixup, we check performance of the model on linear combinations of input samples within the same label. It is important that the perturbations are 'valid', without which the network would move into a region of the feature manifold that it has never seen before. Identifying such 'valid' perturbations is difficult, and amounts to finding the independent causal components in the input image and identifying valid interventions on these. A naïve way of doing this is to take linear combinations of input samples, since this will only perturb input samples in directions the network has already seen. We use Mixup also as a proxy for the ratio of random labels in the training data, based on the presumption that linear combinations of samples where even one sample is randomly labelled will be misclassified by the model. |
|
(3) Margin Distribution to measure separation of representations
The margin distribution, an idea taken from traditional shallow learning approaches like SVMs, has been shown to be correlated to generalization. The margin distribution at an intermediate layer is a measure of how far away samples are from being classified into another class. We demonstrate that the augmented margin distribution is a much better metric at predicting generalization, and can take into account overfitted and outlier samples. We compare various augmentations including image augmentations, adverserial perturbations, and mixup, and evaluate them to see which of these provides most value for predicting generalization. |